Исходные данные:
Перекрытие из деревянных балок сечением 20×5 см, с шагом Ш= 0,58 м
Длина пролета 3,7 м
допустимый прогиб 1/200
Общая приведенная распределенная нагрузка на перекрытие q = 400 кг/м².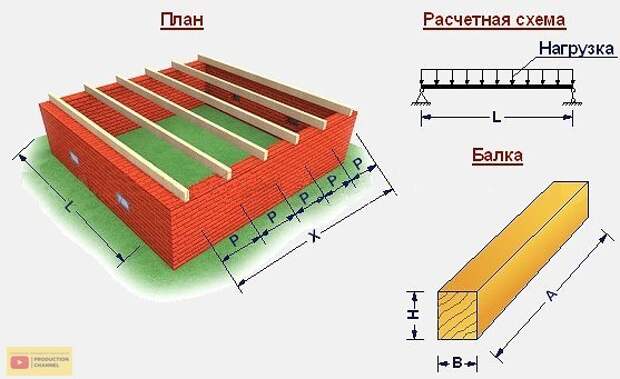 
M_max=(q_(пог.)∙〖L_р〗^2)/8=(232∙〖3,7〗^2)/8=397,01 кгс∙м=39701 кгс∙см
qпог = q×Ш= 400×0,58=232 кг*м
определяем требуемый момент сопротивления деревянной балки
Wтреб = Мmax / R,
где R -расчетное сопротивление древесины хвойных пород на изгиб
R = 14 МПа = 142,71 кгс/см²
Wтреб = 39701 / 142,71 = 278,19 см³
Wбалки ≥ Wтреб
Wбалки = b x h² / 6 = 5×20²/6= 333,33 см³ ≥ 278,19 см³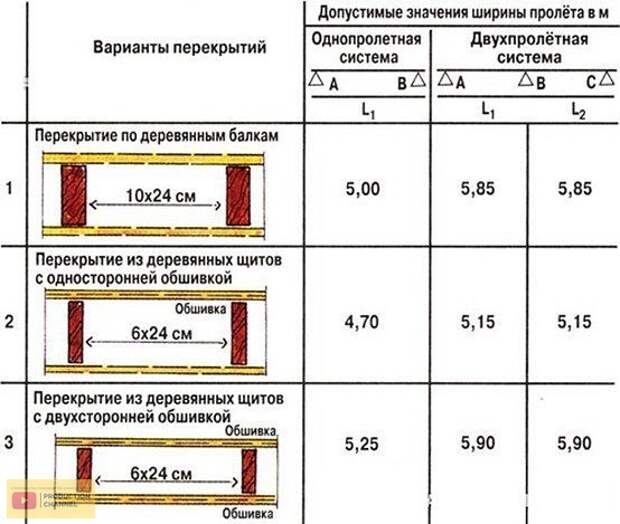 
Условие выполняется.
Определение прогиба балки. 
f=(5ql4)/(384EJ)
где q - нагрузка на балку
l - расстояние между несущими стенами
Е - Модуль упругости древесины, при расчете по предельным состояниям второй группы следует принимать равным вдоль волокон Е = 10 000 МПа (100 000 кгс/см2 или 10х10^8 кгс/м²)
J - момент инерции, для доски прямоугольного сечения
J = b x h³ / 12 = 5 х 20³ / 12 = 3333,33 см4
f = 5 х 232 х 3,74 / 384 х 10 х 10^8 х 3333,33 х 10-8 = 0,017 м или 1,7 см.
допустимый прогиб f доп=L/200=370/200=1,85см≥1,7см Условие по прогибу выполняется.
Определение прогиба балки от точечной нагрузки приложенной к её центру.
f_max=(P∙l³)/48EJ
J = b x h³ / 12 = 5 х 20³ / 12 = 3333,33 см4
f = 240 кг х 3,7м3 / 48 х 10 х 10^8 кг/м²х 3333,33 х 10-8 м⁴= 0,0076 м или 0,76 см.
Свежие комментарии